La Value At Risk (VAR)
Naissance de la Value At Risk
Utilisée pour la première fois dans les années 1980 par la banque Bankers Trust sur les marchés financiers américains, la notion de Value-At-Risk (ou VAR) a principalement été démocratisée par la banque JP Morgan dans les années 1990 grâce à son système de RiskMetrics.
Jusqu’alors, les méthodes utilisées pour détecter et gérer les risques de marché ne permettaient pas de comparer les mesures de risque entre les différentes activités de marché.
L’accroissement de la volatilité des marchés financiers, le développement des produits dérivés et surtout une série de faillites et de krachs boursiers ont poussé les institutions financières à mettre en place un indicateur commun et synthétique des risques financiers.
Il faudra attendre 1995 et les accords de Bâle, pour voir la concrétisation et l’émergence de ce nouvel indicateur considéré très rapidement comme un standard dans l’évaluation des risques financiers.
Définition
La Value-At-Risk représente la perte potentielle maximale d’un investisseur sur la valeur d’un actif ou d’un portefeuille d’actifs financiers qui ne devrait être atteinte qu’avec une probabilité donnée sur un horizon donné.
Elle est, en d'autres termes, la pire perte attendue sur un horizon de temps donné pour un certain niveau de confiance.
La VAR peut être considérée comme un quantile de la distribution de pertes et profits associée à la détention d’un actif ou d’un portefeuille d’actifs sur une période donnée.
Si l’on considère un taux de couverture de a% (souvent 95% ou 99%), la VAR à un jour correspond au quantile de niveau a% de la distribution de pertes et profits sur la période de détention d’un actif.
La Value-At-Risk dépend en réalité de trois éléments
1) La distribution des pertes et profits du portefeuille valable pour une certaine période de détention et dont les différentes méthodes de calcul seront expliquées un peu plus loin dans cette fiche.
2) Le niveau de confiance.Compris entre 0 et 1, il permet de contrôler la probabilité que l’on obtienne un rendement supérieur ou égal à la VAR.
Supposons par exemple que la distribution des pertes et profits associée à la détention d’un actif sur une période corresponde à une distribution normale standard.
La VAR au seuil de confiance de 95% à 1 jour notée VAR(95%, 1Jour), égale à 1 million d’euros signifie qu’il y a 95% de chances pour que la perte associée à la détention de l’actif n’excède pas 1 million d’euros.
Graphiquement, la VAR un jour avec un indice de confiance de 95% peut être représentée par le graphique ci-dessous:
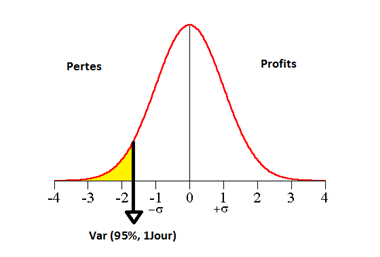
D'après ce graphique, la VAR(95%, 1Jour) correspond à une perte approximative de 1,65 million d’euros.
3) La période de détention de l’actif ou du portefeuille d’actifs.
Le calcul de la VAR doit être ajusté de façon à tenir compte de la composition des rendements. Même si la période de détention est propre à chacun, les autorités de régulation exigent des horizons communs dans le cadre des procédures de validation de la Value-At-Risk.
A qui cette mesure est-elle destinée ?
Utilisée principalement par les banques, cette mesure de risque est destinée avant tout :
- Aux professionnels de marchés tels que les opérateurs de marché, gestionnaires de fonds privés ou encore gestionnaires de fonds institutionnels.
- Aux Risk Managers (responsables de la gestion des risques et du contrôle de la gestion des risques).
- Aux comptables ou aux clients institutionnels.
Hypothèses nécessaires au calcul de la VAR
La détermination de la Value-At-Risk repose principalement sur trois hypothèses:
- La première hypothèse, et non des moindres, concerne la normalité des distributions considérées. On suppose généralement que le prix d’un instrument financier suit une loi log-normale.
- La deuxième hypothèse concerne le lien entre une VAR à N jours et une VAR à 1 jour. En effet on considère que la VAR à N jours est égale à la racine carré de N multipliée par la VAR 1 jour.
- Enfin, la dernière hypothèse est que le rendement moyen d’un actif financier est nul pour la période considérée. (Si l’on s’attend à un rendement annuel moyen de 15% pour un certain actif, le rendement journalier moyen est de 15/252=0,06%, 252 correspondant au nombre de jours où la bourse est ouverte. Ainsi faire l’hypothèse d’un rendement journalier nul n’est donc pas restrictif).
Les différentes méthodes d’estimation de la distribution de pertes (calcul de la VAR)
- La méthode historique nécessite seulement de connaître la valeur de la position dans le passé (par exemple historique des prix pour un indice). Pour un portefeuille, il faudra reconstituer sa valeur passée à partir du prix des différents actifs et de la composition actuelle du portefeuille. Après avoir identifié les facteurs de risque significatifs pour le portefeuille, on utilise l'historique des données collectées afin d'en déduire un montant de perte.
Exemple: Soit un portefeuille composé de plusieurs actifs. Afin de calculer la VAR historique à un jour sur ce portefeuille il faut relever l'ensemble des gains et des pertes quotidiennes réalisées sur les 1 000 derniers jours (par exemple). Une fois toutes ces données obtenues, il faut les classer par ordre croissant. Si l'on souhaite obtenir la VAR à 99%, il suffira de trouver la 10ème (1000*(100%-99%)) valeur obtenue.
Avantages et inconvénients de cette méthode :
Cette méthode est très peu coûteuse en calcul et en technique. De plus aucune hypothèse préalable sur la forme de la distribution n’est requise.
En revanche, cette simplicité de mise en place, engendre de nombreuses limites. Et ce qui peut être considéré comme un avantage peut rapidement se retourner en inconvénient. En effet, l’historique doit être suffisamment grand comparé à l’horizon de la VAR et à son niveau de confiance, mais pas trop pour s’assurer que la loi de probabilité n’a pas trop changé sur la période. Autre point négatif, et non des moindres, cette méthode est inadaptée aux produits dérivés.
- La deuxième méthode de calcul de la VAR est la méthode analytique ou paramétrique. Basée sur des calculs statistiques elle consiste avant tout à définir une formule décrivant la distribution des pertes et des profits.
Cette méthode repose sur plusieurs hypothèses:
1) Les variations des facteurs de risques suivent une loi normale.
2) La relation entre les variations des valeurs du portefeuille et les variations des valeurs du marché est linéaire.
3) Les produits dérivés sont linéaires et les obligations peuvent être ramenées à des pay-offs linéaires. La seule exception à cette condition étant les options.
Exemple 1:
Soit deux portefeuilles ![]() de 1 million d'euros et
de 1 million d'euros et ![]() de 5 millions d'euros constitués respectivement d'actions Peugeot, de volatilité annuelle 20%, et d'actions Société Générale de volatilité annuelle 10%.
de 5 millions d'euros constitués respectivement d'actions Peugeot, de volatilité annuelle 20%, et d'actions Société Générale de volatilité annuelle 10%.
La volatilité quotidienne du portefeuille A est : ![]()
où 252 est le nombre de jours où la bourse française est ouverte.
Ainsi la Var à 99% à une journée est alors : ![]()
La volatilité quotidienne du portefeuille B est: ![]()
Et la Var à 99% à une journée est donc : ![]()
Afin d'obtenir la Var à 10 jours il suffit d'appliquer la formule: ![]()
Ainsi : ![]()
Un investisseur possédant ces deux actifs dans un même portefeuille, doit prendre en compte la corrélation entre les variations du titre Société Générale et les variations du titre Peugeot.
Considérons que le coefficient de corrélation entre les deux actifs est ρ=0,6.
On peut alors obtenir la Var par la formule suivante :
![]()
Dans notre exemple ![]()
Ainsi on peut remarquer que cette Value at Risk est inférieure à la somme des deux VAR calculées précédemment. Ceci est dû aux gains de diversification.
Remarque: La même logique devra être appliquée à un portefeuille constitué de N actifs (en prenant en compte la corrélation entre chacun d'entre eux).
Avantages et inconvénients de cette méthode
Le principal point fort de cette méthode repose sur la rapidité et la simplicité des calculs qui nécessitent seulement une matrice de variance-covariance entre les différents actifs présents dans le portefeuille.
Mais elle reste inadaptée aux portefeuilles non linéaires (instruments optionnels) et aux distributions non-normales des rendements.
- La dernière méthode n'est autre qu'une méthode de simulation par Monte Carlo et n'est utilisée que lorsque les autres méthodes ne s'appliquent pas. Après avoir identifier les facteurs de risque du portefeuille d'actifs (taux de change, cours d'une action...), il suffit de simuler un grand nombre de fois les valeurs futures possibles de ces facteurs par Monte Carlo, puis de calculer le montant des pertes ou des gains associés à ces simulations.
Exemple 2:
Prenons un exemple relativement simple. Un opérateur souhaite investir sur une action aujourd'hui et la revendre dans un an (espérant ainsi la revendre plus cher qu'il ne l'a acheté). Mais durant ce laps de temps, l'action est soumise à des fluctuations. L'opérateur souhaitant ainsi déterminer la VAR de cette action va simuler par Monte Carlo, 10 000 variations possibles (par exemple), puis calculer les pertes ou les gains réalisés dans chacune de ces simulations.
Si l'opérateur souhaite obtenir une VAR à 99%, il lui suffira de repérer la 100ème pire perte afin de pouvoir affirmer avec 99% de chances que la perte qu'il réalisera sur cette opération ne dépassera pas ce montant.
Points forts et points faibles
Cette méthode permet dans la plupart des cas de calculer la VAR lorsque les autres méthodes ne le permettent pas. Elle convient à tous les types d'instruments y compris les produits optionnels.
En revanche la mise en œuvre de cette méthode de simulation est très lourde et nécessite d'énormes calculs. Ainsi le principal défaut de cette méthode repose sur le temps de calcul nécessaire pour générer un grand nombre de scénarios.
Quels sont les limites de la Value At Risk ?
On vient de voir que la Value At Risk pouvait être considérée comme la perte potentielle maximale. Mais son évaluation repose sur des imprécisions parfois plus ou moins importantes qui peuvent influencer le résultat final.
- La première limite réside dans l'hypothèse de normalité des variations des prix des différents actifs. En effet, la loi normale sous-estime bien souvent les grandes variations de marché et néglige ainsi le caractère leptokurtique des queues de distributions (longues queues de distributions).
- La seconde limite concerne la fiabilité du résultat obtenu lorsque, pour anticiper l'évolution d'un actif dans un avenir plus ou moins proche, on utilise son évolution passée.
- Le calcul de la Value At Risk nécessite un horizon fixe. C'est à dire que l'on considère le marché liquide et que l'on puisse ainsi couper nos positions à l'horizon choisi.
- Enfin la dernière limite de la VAR vient du fait que l'on utilise énormément d'approximations et de simulations. Et malgré la puissance croissante des machines, la volonté de mise en œuvre rapide impose l'utilisation d'approximations.
Conscient des limites que présentent les différents modèles de la VAR, un backtesting et un stresstesting ont été rendu obligatoire afin de vérifier les résultats obtenus. Le système de backtesting consiste à déterminer le nombre de fois où la perte obtenue a été supérieure à la VAR. Si ce nombre est trop important, il faut revoir le modèle utilisé pour le calcul.
Parallèlement à ces backtesting, le comité de Bâle impose également des stress tests, durant lesquels les portefeuilles seront soumis à des conditions extrêmes de marchés (par exemple variation de 100 points de base à la hausse ou à la baisse des taux, augmentation subite de 20% de la volatilité...) afin de scruter leur comportement face à des scénarios fortement négatifs.
Conclusion
Aujourd'hui, pour de nombreux investisseurs, gérer le risque de position se limite à déterminer des stops de sécurité qui leur permettraient ainsi de limiter les pertes. En réalité cette méthode ne permet pas une mesure du risque mais seulement une décision face au risque. Et même si la Value At Risk n'est pas un vrai instrument de prévision, elle permet néanmoins d'obtenir une mesure quantitative du risque.
Utilisée par la plupart des grandes banques mondiales, la VAR tente depuis de nombreuses années de s'imposer comme un outil universel de mesure du risque. Mais les crises financières de ces dernières années sont venues mettre à mal son image. En effet, de nombreuses institutions ont dû revoir leur modèle de calcul de la Value At Risk suite à des pertes colossales dans leurs activités de trading notamment en 2008 lors de la crise des subprimes.
Ainsi de nouveaux modèles plus solides et mieux adaptés aux grosses variations de marchés devront être mis en place durant les prochaines années afin que la VAR puisse enfin s'imposer comme instrument mondial de mesure du risque.
- Introduction
- Théorie moderne du portefeuille
- Le CAPM
- La méthode APT
- Finance comportementale
- Le ratio de Sharpe
- Le ratio de Treynor
- L'alpha de Jensen
- La volatilité et l'écart-type
- La covariance et la variance
- La corrélation
- Le Beta
- La VAR (value at risk)
- Gestion active et passive
- Gestion traditionnelle et alternative
- Exemples de gestion traditionnelle
- Stratégies de gestion alternative
- La formule de kelly
Vous avez aimé cet article ? Partagez-le avec vos amis en cliquant sur les boutons ci-dessous :






 Suivez les marchés avec des outils de pros !
Suivez les marchés avec des outils de pros !