En statistiques comme en finance la variance et la covariance sont deux des principales mesures utilisées pour mener à bien une étude.
Manipulés par l'ensemble des acteurs financiers, ces deux instruments sont considérés comme la base de toute étude de risque qu'il faut connaitre à tout prix avant même d'entreprendre de manipuler un portefeuille d'actif.
Nous allons donc reprendre ces fondamentaux en rappelant les formules mathématiques et leurs propriétés tout en illustrant avec des exemples concrets.
La variance
La variance est, selon la définition classique, la moyenne des carrés des écarts par rapport à la moyenne. En termes plus mathématiques elle peut être considérée comme une mesure servant à caractériser la dispersion d’une distribution ou d’un échantillon.
La formule de la variance est la suivante :

Grossièrement on peut la voir comme la moyenne des carrés moins le carré des moyennes. Cette formule intègre des carrés dans le but d’éviter que les écarts positifs et les écarts négatifs par rapport à la moyenne ne s’annulent.
La dimension de cette mesure étant le carré de la dimension de la moyenne, on utilise plus souvent l’écart-type qui n’est rien d’autre que la racine de la variance.
La dimension de cette mesure étant la dimension du carré de la moyenne, on utilise plus souvent l’écart-type qui n’est rien d’autre que la racine de la variance.
La variance possède différentes propriétés
- Etant calculée comme l’espérance d’un nombre au carré, la variance est toujours positive ou nulle.
- Si la variance est nulle, cela signifie que la moyenne des carrés des écarts par rapport à la moyenne est nulle et donc que la variable aléatoire est une constante.
- V(aX+b)=a²V(X)
- V(X+Y)=V(X-Y)=V(X)+V(Y)
Prenons un exemple pour illustrer le calcul d’une variance en finance.
Exemple sur un actif
Soit l'actif Société Générale dont on a téléchargé ses cotations de clôture à chaque fin de mois durant une année.
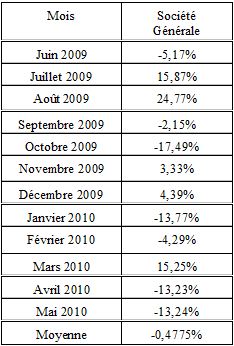
La moyenne des variations est de -0,4775%.
Sa variance est donc: Var (Soc. G.)= (-0,0517+0,004775)²+(0,1587+0,004775)²+(0,2477+0,004775)²+…+(-0,1324+0,004775)²/12=0,01684
Comme la variance est proche de 0 cela signifie que le cours de l’actif ne s’écarte pas énormément de sa moyenne et donc que les variations ne sont pas trop importantes.
Ainsi on dit que la variance traduit la notion d’incertitude. Plus la variance est élevée et plus le cours de l’actif est susceptible de s’éloigner de sa moyenne.
La covariance
La covariance est légèrement différente. Si la variance permet d’étudier les variations d’une variable par rapport à elle-même, la covariance va permettre d’étudier les variations simultanées de deux variables par rapport à leur moyenne respective.
En finance, cette notion permet de mesurer le degré de liaison des fluctuations de deux titres entres eux, ou encore d’un titre avec un indice.
La covariance peut être vue comme le produit des valeurs de deux variables moins le produit des deux moyennes. Mathématiquement, la formule est la suivante :

Du résultat obtenu par cette mesure on en déduit que plus la covariance est faible et plus les séries sont indépendantes et inversement plus elle est élevée et plus les séries sont liées. Une covariance nulle correspondant à deux variables totalement indépendantes.
Exemple concret sur le marché
Prenons un exemple pour illustrer le calcul d’une covariance en finance. Il s'agira ici de comparer deux actions : Air France et Société Générale, dont nous avons récupéré les variations historiques mensuelles.
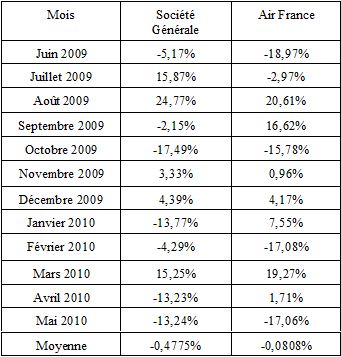
Appliquons la formule de la variance énoncée plus haut, soit :
Cov (Société G.; Air France) = [(-0,0517+0,004775)*(-0,1897+0,000808)+(0,1587+0,004775)*(-0,0297+0,000808)+ ... +(-0,1324+0,004775)*(-0,1706+0,000808)]/12= 0,01074
Avec un résultat positif et pas si faible que cela, on peut en conclure que d'une part ces deux actifs ont évolué de concert, ils sont corrélés positivement. D'autre part, les deux titres ne sont donc pas si indépendants que cela.
La variance d'un portefeuille
A partir de la covariance entre plusieurs actifs ont peut estimer la variance d’un portefeuille de plusieurs actifs. Ainsi la variance d’un portefeuille constitué de N actifs est donnée par la formule suivante :

On obtient donc que la variance d’un portefeuille constitué de N actifs est la somme des covariances de tous les actifs qui le compose, pondérées par la proportion de chacun d’entre eux dans le portefeuille.
Afin de pouvoir appliquer cette formule on doit avant tout calculer la matrice de variance-covariance du portefeuille que l’on détient.
Avec les mêmes notations que pour la formule précédente on obtient la matrice suivante :
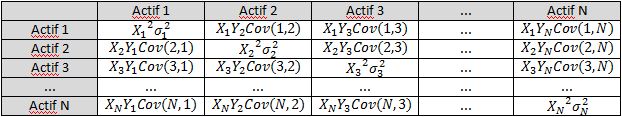
Exemple avec un portefeuille boursier
Soit un portefeuille constitué de 3 actifs dans les proportions suivantes :
- Société Générale 20%
- Air France 30%
- Total 50%
Voici les variations mensuelles de ces trois titres entre juin 2009 et mai 2010:

En utilisant désormais vos connaissances et les résultats des exemples précédents vous obtenez les variances (V) et les covariances (COV) suivantes :
Cov (Société Générale; Air France) = 0,000738
Cov (Air France; Total) = 0,000794
Cov (Société Générale; Total) = 0,000197
V(Société Générale) = 0,01837
V(Air France) = 0,02137
V(Total) = 0,00258
Avec ces éléments on peut construire la matrice de Variance Covariance de notre portefeuille.

En faisant la somme des sous totaux on obtient la variance du portefeuille. Ici, la variance du portefeuille est de 0,00366926.
Son écart type mensuel est obtenu en faisant la racine carré de la variance. Il est donc de : 0,06057442
Et enfin, si l'on veut obtenir l’écart type annuel du portefeuille il suffit de multiplier l’écart type mensuel par racine carré de 12. Ainsi on obtient le pourcentage de risque attendu avec ce portefeuille qui est ici de :0,2098 soit 20,98%.
Ainsi notre portefeuille présente un risque de 20,98%.
En conclusion on peut dire que chacun de ces outils pris indépendamment l’un de l’autre ne sert pas à grand-chose dans la gestion d’un portefeuille. Néanmoins la totalité de ces instruments statistiques reste indispensable afin de pouvoir gérer un portefeuille et abaisser au maximum les risques que l’on prend.




 Suivez les marchés avec des outils de pros !
Suivez les marchés avec des outils de pros !