La théorie moderne du portefeuille, développée par Harry Markowitz dans les années 1950, définit le processus de sélection de titres pour créer le portefeuille le plus efficient possible, c'est à dire qui possède la rentabilité maximum pour un niveau de risque minimum.
Le concept dediversification est à la base de la théorie. En effet, Markowitz pense que les différents titres composant un portefeuille ne peuvent être sélectionnés individuellement et doivent au contraire être choisi selon la corrélation de leurs variations à celles du reste des actifs du portefeuille.
Ce mode de sélection permet de minimiser le risque pour un niveau de rendement choisi.
Analysons les différents composants du modèle :
Makowitz présuppose que les investisseurs sont rationnels et averses au risque et que le marché est efficient. Ainsi, les seuls éléments à prendre en compte sont le risque et le rendement des titres, car les investisseurs achèteront toujours l'actif qui présente un rendement optimal par rapport à son niveau de risque. Aucun investisseur purement rationnel n'achèterait en effet un actif A plus risqué qu'un actif B mais offrant un rendement inférieur.
Dans le modèle, le rendement d'un portefeuille consistera en la somme des rendements des actifs qui le composent, pondérés par leur poids.
Soit :
![]()
Le risque est défini par la volatilité du portefeuille qui correspond à son écart-type :
![]()
avec ![]() la variance que l'on calcule de la manière suivante, pour un portefeuille composé de deux actifs :
la variance que l'on calcule de la manière suivante, pour un portefeuille composé de deux actifs :

avec :![]() : covariance entre les deux actifs que l'on peut exprimer en
: covariance entre les deux actifs que l'on peut exprimer en ![]()
![]() : la variance de l'actif
: la variance de l'actif
et ![]() la corrélation entre les deux actifs
la corrélation entre les deux actifs
Avec ces éléments en main, on peut tester différentes combinaisons d'actifs avec des pondérations diverses pour calculer le risque et la rentabilité espérée d'un portefeuille. La diversification par la sélection d'actifs plus ou moins corrélés permettra d'optimiser cette relation rendement/volatilité.
La frontière efficiente
En définissant les titres par leur rendement et leur niveau de risque, et en illustrant ce rapport sur un graphique, on peut déterminer une frontière efficiente sur laquelle se situent les portefeuilles composés de titres individuels offrant le meilleur rendement pour un certain niveau de risque.
Le portefeuille situé sur la frontière efficiente offre l'espérance de rendement maximale que l'on peut obtenir en pondérant l'investissement effectué dans les différents titres.

Ainsi, seuls les portefeuilles situés sur cette ligne devraient logiquement intéresser les investisseurs rationnels.
L'actif sans risque et la ligne d'allocation des actifs
L'actif sans risque correspond aux obligations étatiques supposées sans risque, qui payent donc le taux minimal. C'est actif a par définition une variance égale à 0 et son rendement n'est pas corrélé aux autres actifs. Ainsi, les différentes combinaisons de l'actif sans risque avec un autre actif donneront une différence de rendement linéaire selon le risque choisi.
On peut représenter l'introduction de l'actif sans risque dans le portefeuille par une demi-droite tangente à l'hyperbole formée par la frontière efficiente. L'extrémité gauche de la demi-droite représente un portefeuille composé uniquement d'actif sans risque. Plus on remonte, plus la proportion en actif sans risque dans le portefeuille diminue et celle en actifs risqués optimum augmente. Au niveau du point de tangence, le portefeuille optimal est composé à 100% d'actifs risqués, et au delà, l'actif sans risque est cette fois emprunté et le portefeuille possède donc un effet de levier.
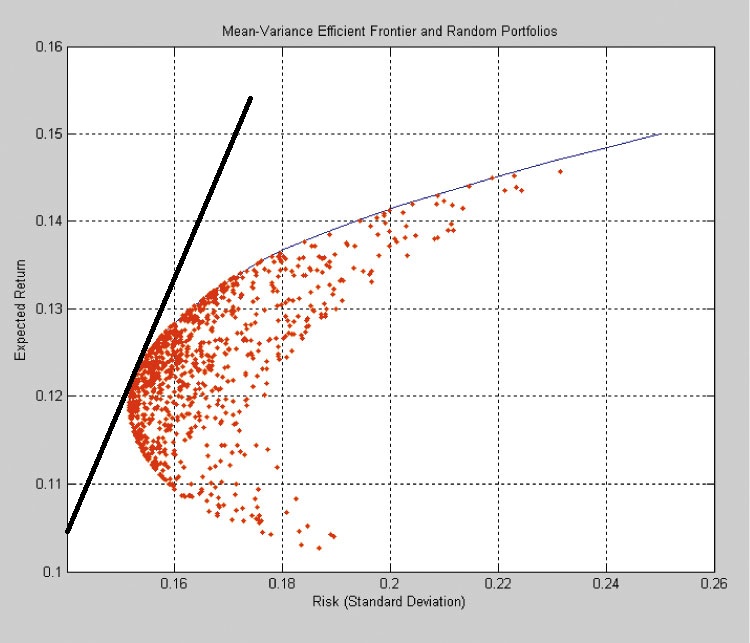
Ainsi, l'investisseur devra choisir un portefeuille sur cette droite de tendance selon le risque choisi : moins risqué en y intégrant de l'actif sans risque, ou plus risqué avec un effet de levier.
Cette méthode de sélection des actifs est-elle optimale ?
De nombreuses critiques se sont élevées à l'encontre de la méthode de Markowitz, notamment portées par le fait que le modèle est basé sur une distribution gaussienne des rendements des titres, ce qui est empiriquement faux, et que la corrélation entre les actifs d'un portefeuille, présupposée stable dans le modèle est en fait en variation constante dans la réalité.
La théorie présuppose également un monde parfait constitué d'investisseurs purement rationnels opérant dans un marché efficient, ce qui est bien entendu illusoire.
Néanmoins, la théorie moderne du portefeuille a constitué une avancée importante dans la modélisation mathématique financière, et Markowitz a reçu le prix Nobel en sciences économiques pour ses travaux en 1990.




 Suivez les marchés avec des outils de pros !
Suivez les marchés avec des outils de pros !