La corrélation, un outil de gestion du risque

Définition

La corrélation entre deux actifs financiers, ou plus généralement entre deux variables aléatoires, est l'intensité de la liaison qu'il existe entre ces deux variables.

Afin de déterminer cette liaison il suffit de calculer le coefficient de corrélation par la formule suivante :

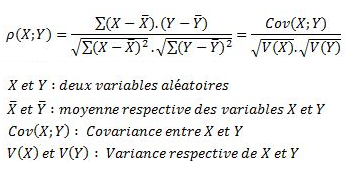
L'interprétation du résultat est relativement simple. Il est tout toujours compris entre +1 et -1.

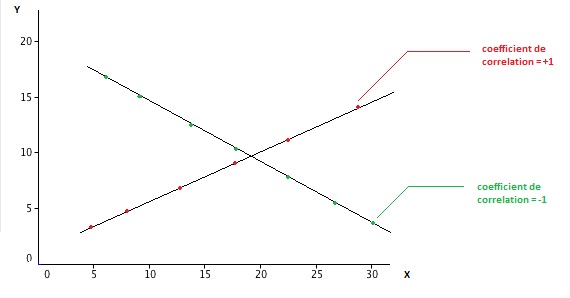
Plus le coefficient est proche des extrémités et plus les variables sont corrélées, c'est à dire dépendantes linéairement l'une par rapport à l'autre.

Un corrélation égale à +1 (respectivement -1) implique qu'il existe une relation linéaire positive (respectivement négative) entre les variables comme le montre le schéma ci dessous. Ceci se traduit par l'existence de 2 réels a et b tels que

Si on dit que les deux variables sont dé-corrélées. C'est à dire qu'il n'existe pas de relation linéaire entre elles (mais il peut très bien en exister une non linéaire).

En revanche on ne doit pas confondre dé-corrélées avec indépendantes. En effet, deux variables indépendantes sont obligatoirement dé-corrélées, mais deux variables dé-corrélées ne sont pas forcément indépendantes. Il se peut qu'il existe une relation non linéaire entre les deux variables.

Plus on se rapproche de (respectivement ) et plus les variables sont corrélées (respectivement anti-corrélées c'est à dire corrélées négativement).

Propriétés

Voici les propriétés du coefficient de corrélation :

• 
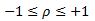
• Si X=Y, alors le coefficient de corrélation est égal à +1.
• le coefficient de corrélation est symétrique. C'est a dire que

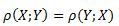
Exemple

Nous allons calculer le coefficient de corrélation entre deux actifs financiers. Nous prendrons les actions Société Générale et Total. Nous étudierons leur corrélation suivant leurs variations mensuelles durant la période juin 2009 à mai 2010.

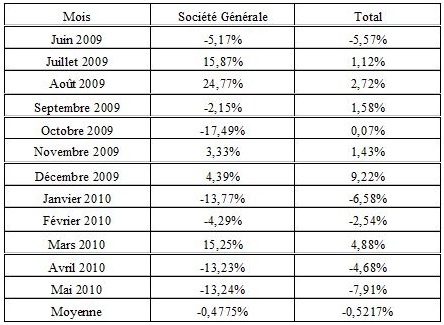
Dans une première étape on calcule la variance de ces deux valeurs, ainsi que leur covariance (pour des explications sur ces notions, voir la fiche Variance/Covariance).

Variance(Société Générale) = (-0,0517+0,004775)²+(0,1587+0,004775)²+(0,2477+0,004775)²+ ... +(-0,1324+0,004775)²/12= 0,016935

De la même manière Variance(Total) = 0,002466

Covariance (Société Générale ; Total) = [(-0,0517+0,004775)*(-0,0557+0,005217)+(0,1587+0,004775)*(-0,0112+0,005217)+ ... +(-0,1324+0,004775)*(-0,0791+0,005217)]/12=0,004217

D'après la formule énoncée au début de cette fiche, le coefficient de corrélation entre les actions Société Générale et Total est de :

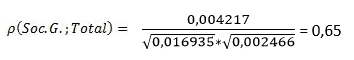
Le coefficient de corrélation entre les deux titres étant assez proche de 1, on peut en conclure que les deux actifs possèdent une relation linéaire entre eux et sont donc relativement corrélés. Les deux valeurs appartenant à l'indice CAC 40, ce n'est au final pas une surprise car il y a un phénomène de groupe dans l'indice.

Remarques

• Le coefficient de corrélation n'est pas sensible aux unités de chacune des variables. Cela signifie que, par exemple, si on étudie la corrélation entre le poids et l'âge d'un individu, le résultat obtenu sera le même si l'on considère l'âge en semaine, en mois ou encore en année.
• Ce coefficient est extrêmement sensible aux valeurs aberrantes ou très éloignées de majorité des autres. Dans ce cas, ces valeurs doivent être retirées des données initiales (on pourra les remplacer par la moyenne de la série.)

Conclusion

Cet outil très simple à manier est régulièrement utilisé en probabilités, en statistique ou encore en finance. En revanche il ne faut jamais perdre de vue que ce n'est pas parce que l'on a obtenu un coefficient de corrélation élevé qu'il existe une relation de cause à effet entre les variables.

Par exemple, malgré la forte corrélation entre le nombre de lunettes de soleil vendues en été avec le nombre de coups de soleil, aucune de ces deux variables n'est la cause de l'autre. Il y a certes un lien, mais on ne peut pas dire de quelle nature.

C'est pourquoi l'utilisateur doit faire un travail supplémentaire sur les données afin de vérifier si le lien n'est pas faussé par une variable extérieure. Ainsi, même s'il est continuellement utilisé et qu'on obtient facilement un résultat, le calcul du coefficient de corrélation devra à chaque fois vérifier la pertinence de ce dernier.